KenKen: Unterschied zwischen den Versionen
***** (***** | *****) |
***** (***** | *****) |
||
| Zeile 29: | Zeile 29: | ||
|- | |- | ||
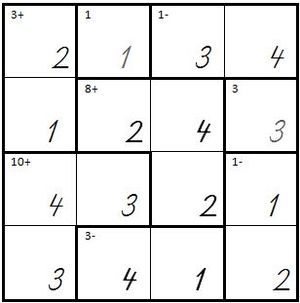
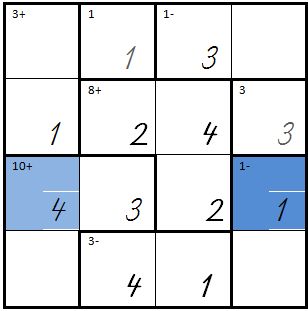
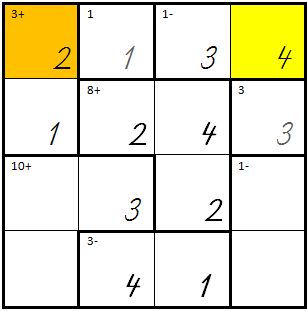
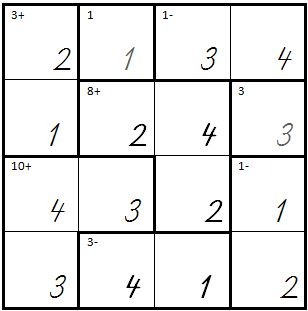
| So sieht ein KenKen mit 3 Spalten und 3 Reihen aus, d.h. es müssen die Zahlen von 1 bis 3 eingetragen werden: | | So sieht ein KenKen mit 3 Spalten und 3 Reihen aus, d.h. es müssen die Zahlen von 1 bis 3 eingetragen werden: | ||
| − | | [[Bild: | + | | [[Bild:KenKen3x3(1).jpg]] |
|- | |- | ||
| | | | ||
| − | | [[Bild: | + | | [[Bild:KenKen3x3(2).jpg]] |
|- | |- | ||
| | | | ||
| − | | [[Bild: | + | | [[Bild:KenKen3x3(3).jpg]] |
|- | |- | ||
| | | | ||
| − | | [[Bild: | + | | [[Bild:KenKen3x3(4).jpg]] |
|- | |- | ||
| | | | ||
| − | | [[Bild: | + | | [[Bild:KenKen3x3(5).jpg]] |
|} | |} | ||
== 2. Beispiel mit Tipps == | == 2. Beispiel mit Tipps == | ||
Version vom 4. Februar 2010, 21:21 Uhr
| Kurzinfo: |
|---|
Inhaltsverzeichnis |
KenKen
KenKen [1] wurde von dem japanischen Lehrer Tetsuya Miyamoto für seine Schüler entwickelt. Es schult die Grundrechenarten, logisches Denken.
Regeln
KenKen ähnelt SuDoku.
- Die Anzahl der Spalten gibt an, welcher Zahlenbereich verwendet wird. Also werden bei 4 Spalten die Zahlen 1 bis 4 verwendet.
- In jeder Zeile und jeder Spalte darf jede Zahl nur einmal vorkommen.
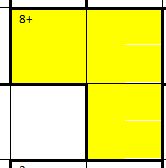
- Zusammengehörende Felder sind stark umrahmt. Hier 3 Felder (siehe Bild rechts)
- Die kleine Zahl in diesen zusammengehörenden Feldern zeigt das Ergebnis. Es gibt die 4 Grundrechenarten (addieren, subtrahieren, multiplizieren, dividieren), die Art wird hinter dem Ergebnis angezeigt. Hier muss die Summe aus den 3 Zahlen 8 ergeben.
1. Beispiel mit Erläuterungen
| Erklärung | Bild |
|---|---|
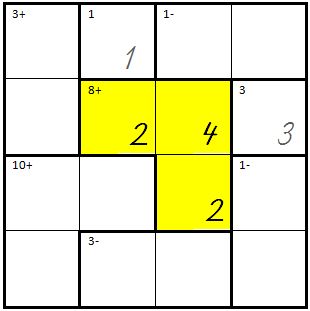
| So sieht ein KenKen mit 3 Spalten und 3 Reihen aus, d.h. es müssen die Zahlen von 1 bis 3 eingetragen werden: | 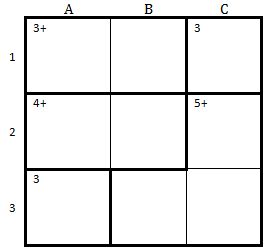
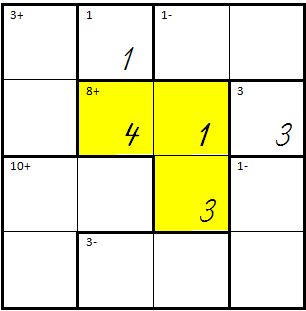
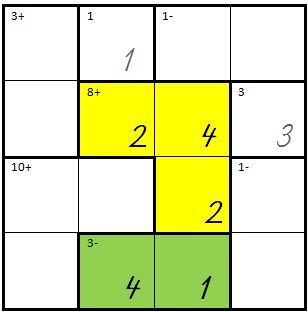
|
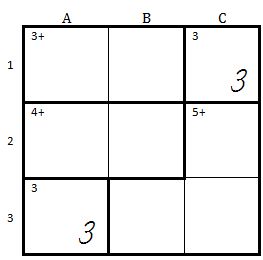
| |
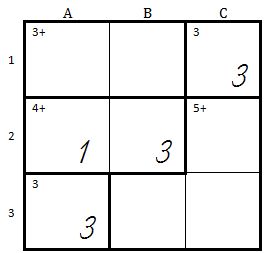
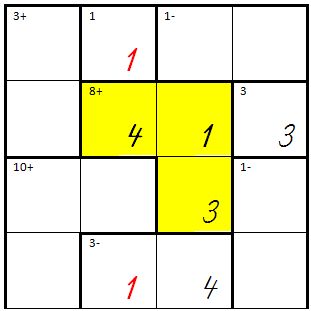
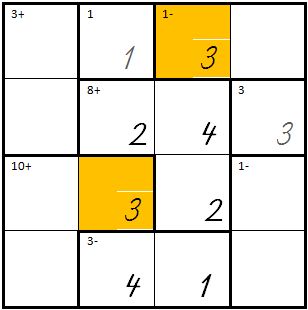
| |
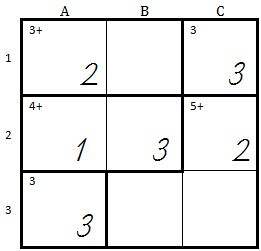
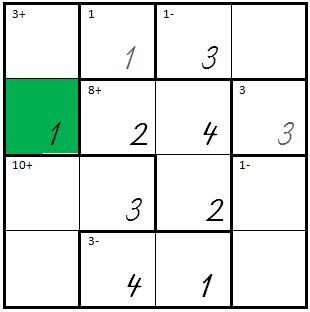
| |
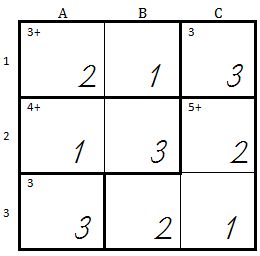
|
2. Beispiel mit Tipps
Bemerkungen des Moses Verlages
| Aus dem Text des Verlags
12px Ursprünglich entwickelte Tetsuya Miyamoto die Rätsel, um Grundschulkinder optimal auf die in Japan sehr entscheidende Aufnahmeprüfung zu den weiterführenden Schulen vorzubereiten. Schnell stellte sich heraus, dass die Kinder nicht nur in Mathe, sondern auch in allen anderen Fächern besser wurden und allgemein selbstbewusster an Probleme herangingen – KenKen ist eben viel mehr als nur ein Zahlenrätsel. Daher war es nur eine Frage der Zeit, bis KenKen auch Lehrern und Eltern in die Hände fiel: Der Faszination und Herausforderung konnten auch sie sich nicht entziehen. Seitdem entwickelt Miyamoto immer komplexere Rätsel und jettet um die Welt, um die KenKen-Philosophie zu verbreiten. 12px |
Links
Bücher zu KenKen:
- moses. Verlag
- Empfehlenswerte Bücher: Katalogsuche Kenken im Moses. Verlag
Weitere Links:
- kenken.com
- nytimes.com/kenken
- Kenken in Facebook Man muss sich bei Facebook anmelden. Die Seite ist in Englisch. Interaktive Beispiele und auch ein Lernvideo.
- ↑ “KenKen® is a registered trademark of Nextoy, LLC, ©2010, KenKen Puzzle LLC”. All rights reserved.
Hier geht es zurück zur Lexikonseite K