KenKen: Unterschied zwischen den Versionen
***** (***** | *****) |
***** (***** | *****) (-doppelte Überschrift) |
||
| (36 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| − | + | {{Babel-1|Lehrer_Verfasser}} | |
| − | + | [[Bild:Kenkenlogo 75dpi.JPG|thumb]] | |
| − | + | [[Bild:Tetsuya Miyamoto.jpg|thumb|Der "Erfinder" von KenKen: Tetsuya Miyamoto]] | |
| − | + | '''KenKen''' <ref>“KenKen® is a registered trademark of Nextoy, LLC, ©2010, KenKen Puzzle LLC”. All rights reserved.</ref> wurde von dem japanischen Lehrer Tetsuya Miyamoto für seine Schüler entwickelt. Es schult die Grundrechenarten, logisches Denken. | |
| + | |||
| + | == Regeln == | ||
| + | KenKen ähnelt SuDoku. | ||
| + | [[Bild:Kenken11.jpg|thumb|Fertig ausgefülltes KenKen]] | ||
| − | + | [[Bild:Kenken00.jpg|thumb|Nur 3 Felder aus obigem KenKen]] | |
| + | # Die Anzahl der Spalten gibt an, welcher Zahlenbereich verwendet wird. Also werden bei 4 Spalten die Zahlen 1 bis 4 verwendet. | ||
| + | # In jeder Zeile und jeder Spalte darf jede Zahl nur einmal vorkommen. | ||
| + | # Zusammengehörende Felder sind stark umrahmt. ''Hier 3 Felder'' (siehe Bild rechts) | ||
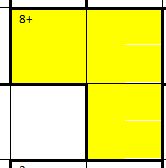
| + | # Die kleine Zahl in diesen zusammengehörenden Feldern zeigt das Ergebnis. Es gibt die 4 Grundrechenarten (addieren, subtrahieren, multiplizieren, dividieren), die Art wird hinter dem Ergebnis angezeigt. ''Hier muss die Summe aus den 3 Zahlen 8 ergeben.'' | ||
| − | [[Bild:Kenken02.jpg]] | + | == Erstes einfaches Beispiel mit Erläuterungen == |
| + | {| class="prettytable" | ||
| + | ! Erklärung | ||
| + | ! Bild | ||
| + | |- | ||
| + | | So sieht ein KenKen mit 3 Spalten und 3 Reihen aus, d.h. es müssen die Zahlen von 1 bis 3 eingetragen werden: | ||
| + | | [[Bild:KenKen3x3(1).jpg]] | ||
| + | |- | ||
| + | | | ||
| + | | [[Bild:KenKen3x3(2).jpg]] | ||
| + | |- | ||
| + | | | ||
| + | | [[Bild:KenKen3x3(3).jpg]] | ||
| + | |- | ||
| + | | | ||
| + | | [[Bild:KenKen3x3(4).jpg]] | ||
| + | |- | ||
| + | | | ||
| + | | [[Bild:KenKen3x3(5).jpg]] | ||
| + | |} | ||
| + | == Zweites Beispiel mit Tipps == | ||
| + | |||
| + | |||
| + | {| class="prettytable" width="700px" | ||
| + | ! Erklärung | ||
| + | ! Bild | ||
| + | |- | ||
| + | | So sieht ein KenKen mit 4 Spalten und 4 Reihen aus, d.h. es müssen die Zahlen von 1 bis 4 eingetragen werden: | ||
| + | | [[Bild:Kenken01.jpg]] | ||
| + | |- | ||
| + | | Es gibt Felder ohne Rechenzeichen. In diese Felder kann die Zahl gleich eingetragen werden. | ||
| + | | [[Bild:Kenken02.jpg]] | ||
| + | |- | ||
| + | | Die Summe 8 kann erzeugt werden durch: 2+3+3, geht aber nicht, weil die 3 in dieser Zeile schon verbraucht ist | ||
| + | 1+3+4, könnte eingegeben werden, wobei logischerweise in der 2. Spalte nur die 4 eingetragen werden kann, die 3 geht nicht, weil sonst in der Zeile zwei Mal die 3 steht, die 1 geht nicht, weil sonst in der 2. Spalte zwei Mal die 1 stehen würde. | ||
| + | | [[Bild:Kenken03.jpg]] | ||
| + | |- | ||
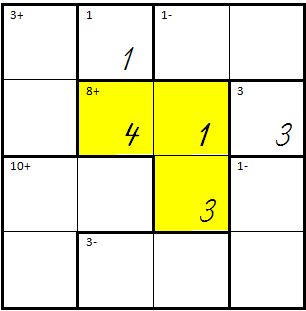
| + | | Jetzt muss in der letzten Zeile die Differenz aus 2 Zahlen 3 ergeben, das geht nur mit 4-1=3<br/> | ||
| + | wobei logischerweise in der 3. Spalte, 4. Zeile nur die 4 eingetragen werden kann.<br />Die Eintragung ist z.B. so möglich, aber dann ergeben sich in der 2. Spalte zwei Mal die 1. <br />→ '''Folgerung:''' So geht es nicht. In den 3 gelben Zellen müssen andere Zahlen eingetragen werden. | ||
| + | | [[Bild:Kenken04.jpg]] | ||
| + | |- | ||
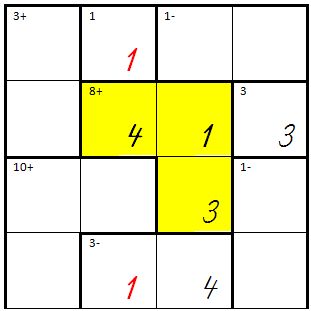
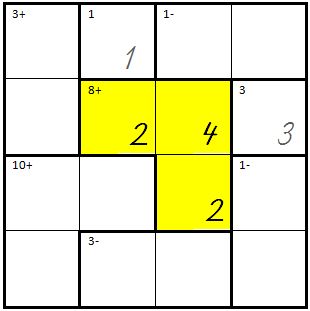
| + | | Die Summe kann auch mit 4+2+2=8 errechnet werden. <br />'''Merke:'''Die gleichen Zahlen müssen so eingegeben werden. | ||
| + | | [[Bild:Kenken05.jpg]] | ||
| + | |- | ||
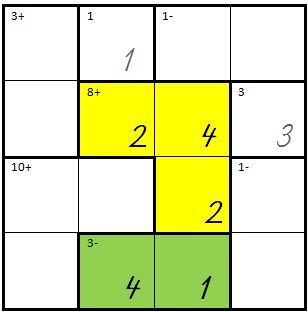
| + | | Dann bleibt für die letzte Zeile, hier grün eingefärbt, die Eingabe von 4 und 1: | ||
| + | | [[Bild:Kenken06.jpg]] | ||
| + | |- | ||
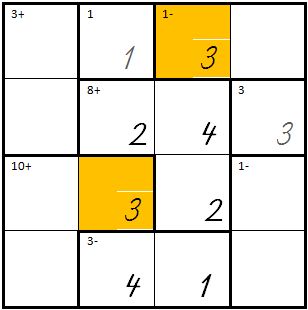
| + | | Dann ergeben sich für die orangen Felder die Zahlen 3: | ||
| + | | [[Bild:Kenken07.jpg]] | ||
| + | |- | ||
| + | | Dann ergibt sich für das grüne Feld die Zahl 1: | ||
| + | | [[Bild:Kenken08.jpg]] | ||
| + | |- | ||
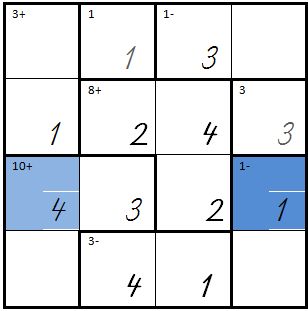
| + | | In den blauen Feldern müssen dann die Zahlen 4 und 1 stehen, andere Zahlen sind waagrecht schon belegt: | ||
| + | | [[Bild:Kenken09.jpg]] | ||
| + | |- | ||
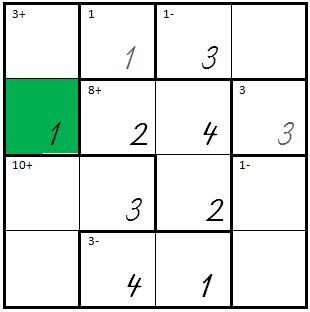
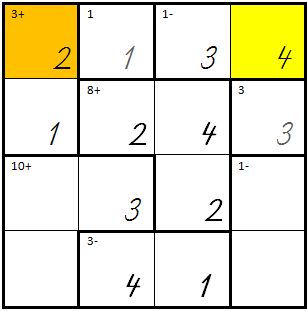
| + | | Links oben als Summe 3 muss die Zahl 2 (oranges Feld) und ganz rechts die Zahl 4 (gelbes Feld) eingetragen werden: | ||
| + | | [[Bild:Kenken10.jpg]] | ||
| + | |- | ||
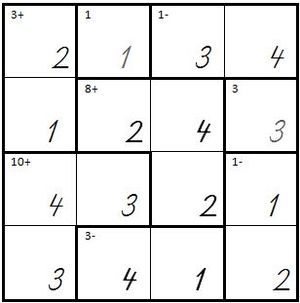
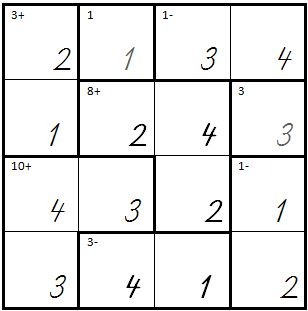
| + | | Das fertige KenKen sieht dann so aus:<br />Als Kontrolle kann man die Summe 10 aus 3+4+3 errechnen und die Differenz 1 muss aus 2 und 1 gebildet worden sein. | ||
| + | | [[Bild:Kenken11.jpg]] | ||
| + | |} | ||
| + | |||
| + | == Bemerkungen des Moses Verlages == | ||
| + | [[Bild:Moses Logo 72ppi rgb.jpg|thumb]] | ||
| + | |||
| + | {{Zitat float|Aus dem Text des Verlags| | ||
| + | Ursprünglich entwickelte Tetsuya Miyamoto die Rätsel, um Grundschulkinder optimal auf die in Japan sehr entscheidende Aufnahmeprüfung zu den weiterführenden Schulen vorzubereiten. | ||
| + | |||
| + | Schnell stellte sich heraus, dass die Kinder nicht nur in Mathe, sondern auch in allen anderen Fächern besser wurden und allgemein selbstbewusster an Probleme herangingen – KenKen ist eben viel mehr als nur ein Zahlenrätsel. | ||
| + | |||
| + | Daher war es nur eine Frage der Zeit, bis KenKen auch Lehrern und Eltern in die Hände fiel: Der Faszination und Herausforderung konnten auch sie sich nicht entziehen. Seitdem entwickelt Miyamoto immer komplexere Rätsel und jettet um die Welt, um die KenKen-Philosophie zu verbreiten. | ||
| + | }} | ||
| + | <!--Die folgenden Bemerkungen müssen aus Copyrightgründen im Text bestehen bleiben--> | ||
| + | <!--Beginn Geschützt--> | ||
| + | |||
| + | == Links == | ||
| + | |||
| + | '''Bücher zu KenKen: | ||
| + | * ''' [http://www.moses-verlag.de moses. Verlag] | ||
| + | * Empfehlenswerte Bücher: [https://shop.moses-verlag.de/catalogsearch/result/?q=kenken&x=0&y=0 Katalogsuche Kenken im Moses. Verlag] | ||
| + | |||
| + | |||
| + | '''Weitere Links:''' | ||
| + | * [http://www.kenken.com kenken.com] | ||
| + | * [http://www.nytimes.com/kenken nytimes.com/kenken] | ||
| + | * [http://apps.facebook.com/_kenken_/ Kenken in Facebook] Man muss sich bei Facebook anmelden. Die Seite ist in Englisch. Interaktive Beispiele und auch ein Lernvideo. | ||
| + | |||
| + | <!--Ende geschützt--> | ||
| + | |||
| + | <references /> | ||
| + | |||
| + | {{Rücksprung|K}} | ||
Aktuelle Version vom 19. Februar 2010, 21:12 Uhr
| Kurzinfo: |
|---|
KenKen [1] wurde von dem japanischen Lehrer Tetsuya Miyamoto für seine Schüler entwickelt. Es schult die Grundrechenarten, logisches Denken.
Inhaltsverzeichnis |
Regeln
KenKen ähnelt SuDoku.
- Die Anzahl der Spalten gibt an, welcher Zahlenbereich verwendet wird. Also werden bei 4 Spalten die Zahlen 1 bis 4 verwendet.
- In jeder Zeile und jeder Spalte darf jede Zahl nur einmal vorkommen.
- Zusammengehörende Felder sind stark umrahmt. Hier 3 Felder (siehe Bild rechts)
- Die kleine Zahl in diesen zusammengehörenden Feldern zeigt das Ergebnis. Es gibt die 4 Grundrechenarten (addieren, subtrahieren, multiplizieren, dividieren), die Art wird hinter dem Ergebnis angezeigt. Hier muss die Summe aus den 3 Zahlen 8 ergeben.
Erstes einfaches Beispiel mit Erläuterungen
| Erklärung | Bild |
|---|---|
| So sieht ein KenKen mit 3 Spalten und 3 Reihen aus, d.h. es müssen die Zahlen von 1 bis 3 eingetragen werden: | 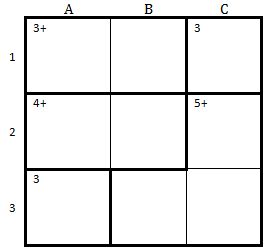
|
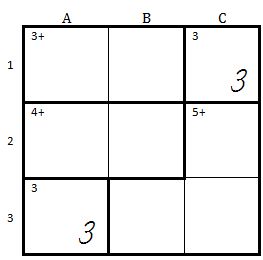
| |
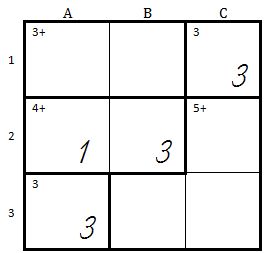
| |
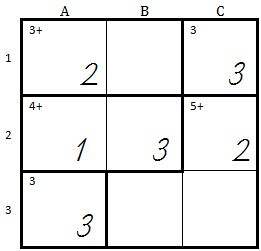
| |
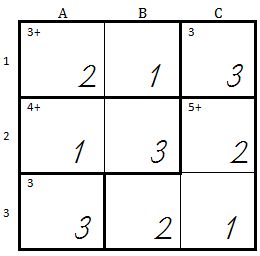
|
Zweites Beispiel mit Tipps
Bemerkungen des Moses Verlages
| Aus dem Text des Verlags
12px Ursprünglich entwickelte Tetsuya Miyamoto die Rätsel, um Grundschulkinder optimal auf die in Japan sehr entscheidende Aufnahmeprüfung zu den weiterführenden Schulen vorzubereiten. Schnell stellte sich heraus, dass die Kinder nicht nur in Mathe, sondern auch in allen anderen Fächern besser wurden und allgemein selbstbewusster an Probleme herangingen – KenKen ist eben viel mehr als nur ein Zahlenrätsel. Daher war es nur eine Frage der Zeit, bis KenKen auch Lehrern und Eltern in die Hände fiel: Der Faszination und Herausforderung konnten auch sie sich nicht entziehen. Seitdem entwickelt Miyamoto immer komplexere Rätsel und jettet um die Welt, um die KenKen-Philosophie zu verbreiten. 12px |
Links
Bücher zu KenKen:
- moses. Verlag
- Empfehlenswerte Bücher: Katalogsuche Kenken im Moses. Verlag
Weitere Links:
- kenken.com
- nytimes.com/kenken
- Kenken in Facebook Man muss sich bei Facebook anmelden. Die Seite ist in Englisch. Interaktive Beispiele und auch ein Lernvideo.
- ↑ “KenKen® is a registered trademark of Nextoy, LLC, ©2010, KenKen Puzzle LLC”. All rights reserved.
Hier geht es zurück zur Lexikonseite K