KenKen: Unterschied zwischen den Versionen
Aus ZUM-Grundschul-Wiki
***** (***** | *****) (→Beispiel mit Tipps) |
***** (***** | *****) (→Beispiel mit Tipps) |
||
| Zeile 36: | Zeile 36: | ||
|- | |- | ||
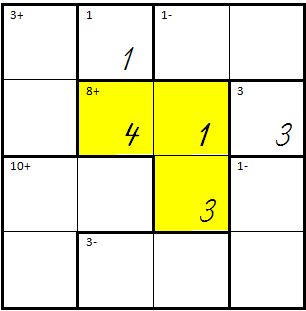
| Jetzt muss in der letzten Zeile die Differenz aus 2 Zahlen 3 ergeben, das geht nur mit 4-1=3<br/> | | Jetzt muss in der letzten Zeile die Differenz aus 2 Zahlen 3 ergeben, das geht nur mit 4-1=3<br/> | ||
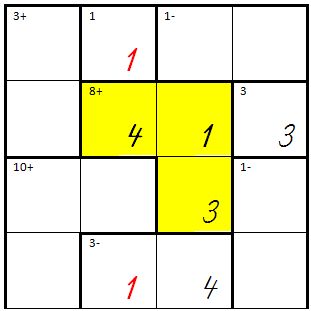
| − | wobei logischerweise in der 3. Spalte, 4. Zeile nur die 4 eingetragen werden kann.<br />Die Eintragung ist z.B. so möglich, aber dann ergeben sich in der 2. Spalte zwei Mal die 1. <br />→ '''Folgerung:''' So geht es nicht. | + | wobei logischerweise in der 3. Spalte, 4. Zeile nur die 4 eingetragen werden kann.<br />Die Eintragung ist z.B. so möglich, aber dann ergeben sich in der 2. Spalte zwei Mal die 1. <br />→ '''Folgerung:''' So geht es nicht. In den 3 gelben Zellen müssen andere Zahlen eingetragen werden. |
| [[Bild:Kenken04.jpg]] | | [[Bild:Kenken04.jpg]] | ||
| + | |- | ||
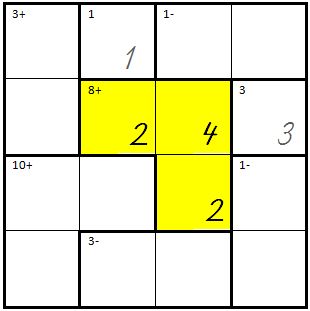
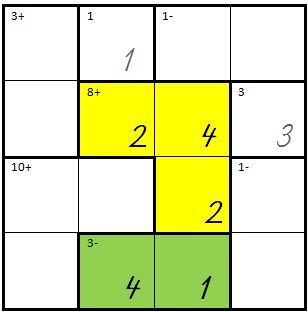
| + | | Die Summe kann auch mit 4+2+2=8 errechnet werden. <br />'''Merke:'''Die gleichen Zahlen müssen so eingegeben werden. | ||
| + | | [[Bild:Kenken05.jpg]] | ||
| + | |- | ||
| + | | Dann bleibt für die letzte Zeile, hier grün eingefärbt, die Eingabe von 4 und 1: | ||
| + | | [[Bild:Kenken06.jpg]] | ||
|} | |} | ||
Version vom 29. Januar 2010, 22:55 Uhr
KenKen
Hier entsteht eine neue Erklärung für KENKEN
Derzeit laufen Verhandlungen mit dem Verlag. -- ***** 18:02, 29. Jan. 2010 (UTC)
KenKen wurde von dem japanischen Lehrer Tetsuya Miyamoto für seine Schüler entwickelt. Es schult die Grundrechenarten, logisches Denken.
Regeln
KenKen ähnelt SuDoku.
- Die Anzahl der Spalten gibt an, welcher Zahlenbereich verwendet wird. Also werden bei 4 Spalten die Zahlen 1 bis 4 verwendet.
- In jeder Zeile und jeder Spalte darf jede Zahl nur einmal vorkommen.
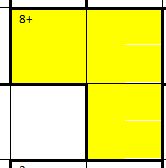
- Zusammengehörende Felder sind stark umrahmt. Hier 3 Felder
- Die kleine Zahl in diesen zusammengehörenden Feldern zeigt das Ergebnis. Es gibt die 4 Grundrechenarten (addieren, subtrahieren, multiplizieren, dividieren), die Art wird hinter dem Ergebnis angezeigt. Hier muss die Summe aus den 3 Zahlen 8 ergeben.